Rolling resistance
Strictly speaking, the construction of the wheel is not finished until the tire is wrapped around it. The rolling resistance of a wheel theoretically decreases with increasing diameter. Wheel diameter here means: the outer size of the inflated tire. Small wheels therefore have a higher rolling resistance, at least if the tire construction and tire pressure are identical. An example where this is clearly visible are the Swallow Stelvio tires; the rolling resistance of the 28 inch version is 40% lower than the 20 inch version.
The rolling resistance of wider tires is theoretically also lower, but because the tirepressure usually decreases, this advantage disappears again. Some manufacturers make multiple tire widths from the same design, e.g. 20, 23 and 25mm; in this case the 25mm version has a somewhat lower rolling resistance at the same pressure. In addition to rolling resistance, a tire also has air resistance and weight; here the narrow tire has the advantage!
The design of the tire (not visible and not easy to measure) and the pressure are the most important factors for rolling resistance. The least important value for the rolling resistance is the tire width! The number of wheels is theoretically unimportant; a tricycle, has a load per wheel that is simply 16.7% lower.
Note: there are very big differences between the various tire constructions; at the same pressure and tire width, one tire can have twice as high a rolling resistance as the other, due to a stiff and thick wall and tread. The most flexible tire is usually the lightest and smoothest running. This is not optimal in terms of punctures and wear.
The surface also counts: rough asphalt and bad road surfaces can more than double the rolling resistance! Especially for small wheels, the rolling resistance increases enormously on rough road surfaces. The rolling resistance coefficient Cr on a smooth concrete floor (e.g. a sports hall) for the following tires is approximately:
Clement Seta tubular 22mm at 8 bar =0,002 / Good racing tire 25 mm at 7 bar = 0,003 / ATB knobby tire 47 mm at 2,5 bar = 0,009 / Puncture-proof tire 37 mm at 5 bar =0,007 / Puncture-proof tire 37 mm at 3 bar = 0,010
On a regular tarmac road, 0,005 is a fair value for a good 25mm racing tire.
The rolling resistance Rrol = m* g* Cr . For the power absorbed by rolling resistance, we must multiply this by speed v (in m / s) and divide by the efficiency of the drivetrain (95% = 0,95). Example: cyclist 70 kg + city bike of 20 kg with anti-puncture tires at 24 km / h: Prol = 90* 9,81* 0,007* 6,67 / 0,95 = 43W. Now put the same cyclist on a real 8 kg racer at the same speed: Prol = 78* 9,81* 0,003* 6,67 / 0,95 = 16W.
Especially at low speeds the rolling resistance has a major impact!
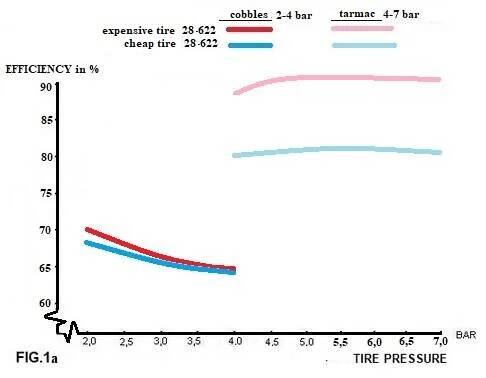
A light rider (incl. bike 75kg) rides over normal asphalt and a cobblestone strip; we measure how efficient the transmission is. We have a cheap tire and an expensive racing tire; on the cobblestones at 2-3-4 bar pressure in the tire, and on asphalt with 4-7 bar. In FIG. 1a. we see a test of how much energy we lose when mounting a cheap tire, or an expensive racing tire under those conditions.
On cobblestones low pressure clearly has the advantage. The difference between the expensive and the cheap tire is not that big. If the road surface is better, that difference increases: at 5 bar, the expensive tire cycles 10% lighter. In other words, John Rich only has to deliver 300W, and Pete Cheap has to pedal 330W for the same 10 m/s speed! On cobblestones, there is less difference ; a lower pressure always gives a somewhat higher efficiency, but punctures are a greater risk at 2 bar.
Certainly anti-puncture tires often have a relatively high rolling resistance; anti-puncture strips also provide extra rolling resistance. Even the choice for a (too) narrow rim gives a higher rolling resistance. Wider tires require wider rims; the inner size should be about half the tire width. Stiff and fat tires like moped tires, have Cr-values close to an ordinary car tire (0,011-0,012).
As indicated, these Cr-values are measured in the laboratory, on smooth concrete or on a large roll. Those figures are easy to reproduce for researchers; differences arise with any road surface. The temperature also has an influence: the colder, the stiffer the tire, the higher the rolling resistance.
In general, a hard-inflated tire will have a lower rolling resistance, but the soil is an important factor here. When we end up on a sandy path with our racing bike, we come to a halt within a few meters. The rolling resistance increases enormously; the deformation of the sand by our racing tires consumes so much energy!
When we ride on an asphalt road with an ATB and 2 bar in the knobby tires, it seems as if someone is permanently pulling our jersey. The deformation of the tires, by pressing on the contact point with the asphalt, consumes energy and thus produces a high rolling resistance. When we ride this bike from the tarmac onto the sandy path, we hardly notice any difference. The pressure per square centimeter of contact surface is much lower. The sand will not deform much, because the contact patch of the tire with the soil is much larger.
Bouncing can also cause significant energy losses. If you hit the cobblestones with rock-hard tires, this is clearly noticeable. In addition to loose bicycle parts and dental fillings, a lot of energy is lost. A wider tire with a lower pressure, keeps in contact with the road and will run lighter on cobbles than an eight bar super light racing tubular.
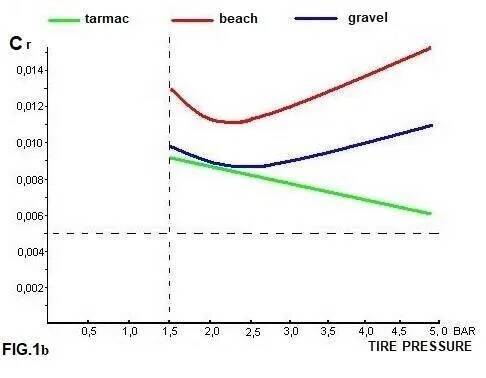
In FIG.1b we see the influence of the terrain on the rolling resistance of various types of surfaces of a 47mm semi-slick ATB tire. It can clearly be seen that the rolling resistance on the road decreases linearly with the increase in tire pressure. Softer surfaces have a higher rolling resistance due to deformation of the soil. In the sand (red line) the resistance increases faster than on the field road (the blue line is flatter). The narrower the tire, the steeper the red and blue curves rise. The minimum Cr in this case is 2- 2,5 bar. This is also a pressure that is used by many ATB'ers; with wide tubeless tires, 0,5 or 1 bar less can be still ridable. If there is a lot of asphalt in the route, you can use a little more pressure; this also applies to a frozen surface.
Fitting a knobby tire instead of the semi-slick increases in rolling resistance by 10% on any terrain. Of course those knobs ensure, that you can deliver your power to the surface, during that muddy climb. Slip once with the semi-slick tire and you will stand still.
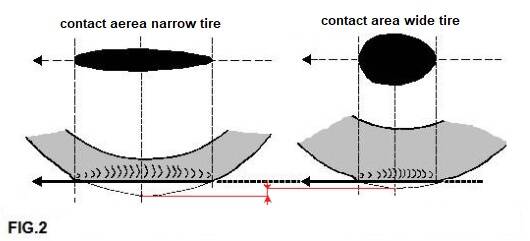
The deformation of a narrow racing tire is relatively high, much greater than that of a wide tire, see FIG. 2. Something resembling a bow wave is created at the front of a rolling tire; the rolling resistance increases as a result. This effect decreases with higher tire pressure.
Distortion absorbs energy; in the nineties there was a company “Greentire”, which sold tires with a solid polyurethane foam filling. Never leaking and lasting a long time; too long, I threw them away before they were worn out. The rolling resistance was enormous due to the energy absorption of the foam. This could be well demonstrated by bouncing the wheel on the floor of the workshop. A racing wheel returns to the same height; the solid tire barely reached half of it. Anti-puncture tires have a reinforcement against penetration by sharp parts. Wolber used to opt for a metal mesh under the tread; nowadays they choose a layer of strong fiber such as Kevlar or Vectran; or an extra tough plastic layer, like Dutchtire and Schwalbe use.
The latest generation of racing tires uses a reinforcement of graphene, a material made up of a single layer of carbon atoms. This promises to deliver an unparalleled product in terms of weight, rolling resistance and puncture resistance. You always hear the best stories about novelties at the introduction; the marketing guys always promise more than the engineers can deliver. The stuff will have to prove it's value and the significant extra expense during competition and everyday use.
With a knobby tire, the knobs will be pushed inwards by the tarmac. The tread and profile of a tire therefore also lead to deformation. For a hard surface, a tire with a slick profile will have a lower rolling resistance. Of course, such a tire is more likely to fail on a muddy climb, but by choosing a lower tire pressure, we can allow the tire to maintain sufficient grip via the knobs on the side of the tread.
Terrain, riding style, weight and personal preference play a major role in the right tire choice.
Narrow racing tires have a high pressure per square centimeter of contact surface with the road; so high that the influence of the profile is nil. A very important factor in the rolling resistance of tires is the flexibility of the sidewall. This is determined by the choice of wire for the carcass. The thinner the fiber, the more fibers per centimeter, the more flexible the tire, the lower the rolling resistance. In old-fashioned tubulars, Egyptian cotton was chosen here, or even pure silk, if lightweight and suppleness were more important than price. The choice for Kevlar is more modern; this is stronger, but also slightly stiffer than cotton or silk; it also replaces the steel wire in the more expensive tires, making the tires foldable.
Vectran HT is a better fiber for tires; at Continental and Swallow they use this in their most expensive racing tires. Graphene promises to dethrone Vectran; in terms of price, that will certainly succeed.
The modern “silica” rubbers used in tires, have more grip on the road surface (especially in the rain), but the rolling resistance is slightly higher. Almost worn tires suffer from fiber breakage, so they are less stiff. They also have less profile; for these reasons they run better than new ones.
Even something like an inner tube influences rolling resistance. The lightest, smoothest and most puncture resistant are old-fashioned latex inner tubes. However, this natural rubber has the disadvantage that it slowly loses pressure. Inflating every day works great, but not everyone likes that; butyl rubbers are slightly stiffer but airtight. Modern butyl rubber mixtures, by the way, are less easy to glue than those old-fashioned inner tubes; the patches don't stick very well! There are new tubes like Schwalbe Aerothan or older polyurethane ones.
In the ATB world the tubeless tires are taking over; that will be the future for all bicycles. The wheel will look different in the coming years; the rim becomes lighter, because disc brakes make the braking surface superfluous. They are going to make airtight tubeless rims; the nipples may disappear from the inside of the rim. By using disc brakes, the dropouts in the frame will be replaced and new parts especially for diskbrakes and the modern thru-axle hubs. Modern rims are hookless, see the video below.
The radial tire has also been brought out of mothballs. The first designs date from 1913. It was only after the Second World War that Michelin developed and produced the first radial car tires. The inventor Rinkowski from the GDR received a patent on radial tires for bicycles in 1950. He made tires on a modest scale for recumbent cyclists and GDR cycling teams. Panaracer also launched a radial tire for cyclists in the 1970s, but it was n't a commercial success. Schwalbe is now doing it with ATB tires; the first stories are positive, but that is often the case with a new product.
EPILOGUE
Rolling resistance measurements are published in many places on the internet and in bicycle magazines. Only studies using the same measuring method are really comparable. This creates differences in data. Nevertheless, a tire that performs well according to method A will also leave most of the competition behind according to method B.
Tire companies release new tires every year, so results will be temporary. Look in archives os cycling magazines or organisations like Human Power.